Introduction to Elliptic curves

Elliptic Curves is a well know concept in cryptographic world which is used in elliptic curve cryptography. Lets start with understanding some basic concepts of elliptic curves which are necessary to understand the undelying concepts of elliptic curve cryptography discussed in subsequent articles.

In cryptography, elliptic curve is a plane curve over a finite field consists of points satisfying the equation given below :
y² = x³ + ax + b
This is the graph of a typical elliptic curve equation.

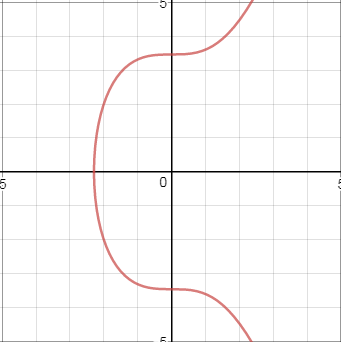
elliptic curve graph

Please Note that elliptic curves are symmetric about the x-axis.

Follow the steps given below to perform addition in elliptic curves :

Draw a line between the points as shown below :

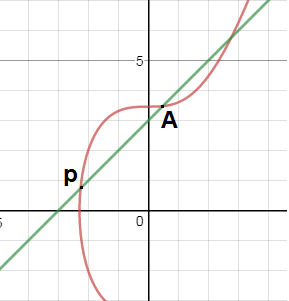
Here we want to add point p and point A .
Mark the Point where the line intersects the elliptic curve as shown below :

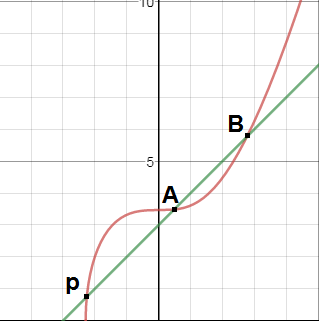
Here Point B is the point where the line intersects.
Reflect the intersection point on the x-axis as shown below :

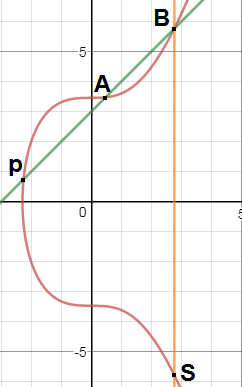
Here Point S is the reflection point of the intersection on the x-axis.

point S is the sum of point p and point A .

Follow the steps given below to perform addition on a single point in elliptic curves :

Draw a line tangent to the point as shown below :

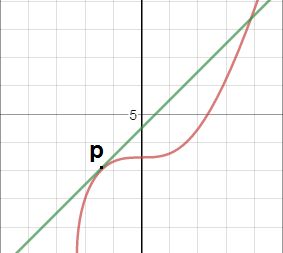
Here we want to add point p with itself.
Mark the Point where the tangent intersects with the elliptic curve as shown below :

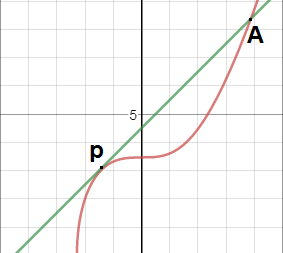
Here Point A is the point where the tangents intersects.
Reflect the intersection point on the x-axis as shown below :

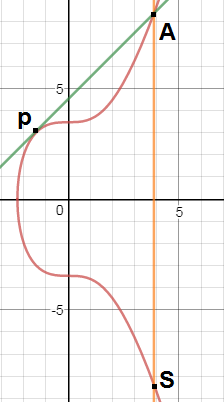
Here Point S is the reflection point of the intersection on the x-axis.

point S is the sum of point p with point p only.

We already learned in the above mentioned example how we can calculate the sum of a point using elliptic curves. As per above example :
Point S = Point p + Point p
i.e.
Point S = 2 * Point p
coz , Multiplication is nothing but adding the number given times.

Now suppose we want to calculate 17 * p so we can calculate it in either of the two ways:

Simple Multiplication :
Point p + point p = Point 2 p
Point 2p + point p = Point 3 p
Point 3p + point p = Point 4 p
Point 4p + point p = Point 5 p
Point 5p + point p = Point 6 p
Point 6p + point p = Point 7 p
Point 7p + point p = Point 8 p
Point 8p + point p = Point 9 p
Point 9p + point p = Point 10 p
Point 10p + point p = Point 11 p
Point 11p + point p = Point 12 p
Point 12p + point p = Point 13 p
Point 13p + point p = Point 14 p
Point 14p + point p = Point 15 p
Point 15p + point p = Point 16 p
Point 16p + point p = Point 17 p
Using this method we computed the result in 17 steps.
Divide and Conquer method :
Point p + point p = Point 2 p
2 * Point 2p = Point 4p
2 * Point 4p = Point 8p
2 * Point 8p = Point 16p
Point 16p + Point p = Point 17p
Using this method we computed the result in only 5 steps which makes it very fast.When the size of the number increases this method becomes more and more useful. This is the reason behind using elliptic curves in cryptographic operations.

Elliptic curve function are trapdoor in nature because multiplication is very fast , however division is very slow.

Basics of elliptical curves